長い疑問「なぜ鏡は左右が逆に映るのか」
「朋(とも)あり遠方より来る、また楽しからずや」
論語です。古い友達と再会する。楽しいことである。と孔子は素直に語っています。
古い友達でなくても、昔々読んだ本と再会するのは、これもまた同じように楽しいものです。
私にとって、そのような本のひとつが、中公新書「詭弁論理学」(野崎昭弘 著)でした。改訂版が出版されているのを最近知り、さっそく手に入れました。
この本は私が学生時代に読んだものなので、ほぼ40年ぶりの友人との再会ということになります。
この本、「論理学」と厳めしい題名がついていますが、内容は至って平易。まったく引っかかるところがありません。とっても消化のいい本です。
人は、議論になるといろいろと詭弁や強弁をつくして相手を言い負かそう、打ち負かそうとします。それに対して、この本では、相手の話を冷静に受け止めて、それが詭弁や強弁であると見抜き、それに対してどのように対処していけばいいのかを教えてくれます。
例えば、この本の中の例を一つ挙げさせてもらいましょう。
ある貴婦人が、宝石店で1万ドルの宝石を買いました。ところが、その宝石を持って家に帰って見直してみると、どうも気に入らない。
それで、翌日、彼女はその宝石を持って宝石店に現れ、その宝石を別のに換えてほしいと頼みました。宝石店はこころよく取り換えを承諾したため、彼女は昨日買った1万ドルの宝石を店に返し、新たに2万ドルの宝石を持って店を出ようとしました。
「奥様、その宝石は2万ドルでございます。昨日お買い上げいただいたのは1万ドルでしたので、差額の1万ドルを支払ってください」
と宝石店の店員が言いました。
すると、その貴婦人はこう答えました。
「あらどうして?昨日1万ドル払ったじゃない。そして、今日1万ドルの宝石をお返ししたので、合計で2万ドルになるはずよ」
もちろんこれは詭弁ですが、そういわれると店員はどう切り返したものか、ハタと困ってしまいます。
この本にはこんな詭弁や強弁が満載。興味ある人は読んでみて下さい。
さて、前置きが随分長くなりましたが、ここからが本題。タイトルに掲げた「鏡はなぜ左右が逆に映るのか」と言う話です。つまり、鏡に映った像は、上下はそのままなのに、左右が逆になってますよね。これはなぜかということです。
これについては、「詭弁論理学」の巻末に書かれています。
ある数学者と物理学者と学生が、この問題について議論すると言う内容です。この議論の中で、いろいろな仮説やら、定義やら、証明やらが飛び出し、なかなか結論が得られない。最後に数学者の意見が物理学者の意見を抑えて議論に勝つわけですが、それはなぜか。
「それは仕方がないんだ、この本はそもそも数学者が書いているのだから、数学者が勝つようになっているんだ」と物理学者が嘆くところがオチになっています。
では数学者はどのように説明したのか。その内容について実は私は全く理解できませんでした。おそらく、この本を読んだほとんどの人は理解できないのではないでしょうか。(理解できたとおっしゃる方がありましたら、申し訳ありません)
私は、この本を閉じたあとも、なぜ鏡は左右が逆に映るのかを考え続けましたが、分かりません。そのまま、思考のジャングルに迷い込み、40年間を過ごすことになってしまいました。(ジュマンジのようにね)
なぜ鏡は左右が逆に映るのか。実はネットでググればいろいろな説が出てきます。ただ、ネットに書かれたどんな説も、私はどうしても理解できないし、納得できません。ここでそれらの説を紹介してもいいのですが、私自身が理解できない話を説明するのは私の主義ではありません。興味ある方はネットでググってみて下さい。
そして、最近、再びこの本を手に取り、改めて考え直してみると、ある解答に行き当たりました。多分、これが正解。以下に説明していきたいと思います。
それは錯覚に過ぎない
では、鏡はなぜ左右が逆に映るのか。結論から先に言えば、それは目の錯覚に過ぎないということです。え~そんな~という声が聞こえて来そうですね。目の錯覚にするなら、どんなことだって説明できるじゃないか。ま~ま~そう言わずに、話を聞いてください。
例えば、あなたが鏡から1m離れて立ったとします。そうすると、鏡の中の1m奥にあなたがこちらを向いて立っている姿が見えるはずです。そう上下はそのまま。でも左右は逆にね。
でも、それは目の錯覚なのです。鏡はガラスの板にアルミや銀をメッキしたものです。ガラス板の厚さは1㎝もないし、アルミや銀のメッキの厚さは数ミクロンしかないでしょう。鏡の中に1mもの奥行きがあるわけでありませんから、鏡面から1m奥にあなたが立っているように見えても、それは目の錯覚なのです。
鏡には奥行きがあって、まるで別の世界が存在するように見えますが、鏡は単に光を反射してるだけです。鏡の中に遠くの像が映っているように見えていても、実際は薄いアルミや銀メッキに映された虚像に過ぎません。
さて、ここで話をしたいのは、奥行きの話ではなく、あなたの像がこちらを向いて立っていると言う点です。私たちは鏡に映った像がまるで、回れ右をして、こちらを向いているように見えます。でもこれも目の錯覚なのです。
決して鏡に映った像は回れ右をして、こちらに向き直ったわけではないのですが、そんな風に見えてしまうのです。そして鏡に映った像が回れ右をしたかのように錯覚しているから、左右が逆になったように見えると言うわけです。
例えば、もしあなたが、前後の区別のない黒い服を着て、頭から黒い布をかぶった状態で鏡の前に立ったところを想像してみて下さい。鏡には真っ黒いあなたのシルエットのような像が見えるはずです。
でも、その像は前を向いているのか、後ろを向いているのかわかりません。だって、あなたは前後の区別のない服を着て黒い布を頭からかぶっているのですから。
この状態で右の手を上げてみて下さい。鏡に映ったあなたの像も手を上げますが、それは右手でしょうか、左手でしょうか。

上の図で示すように、あなたが右手を上げれば、鏡の像も右手を上げています。反転はしていません。 しかし、もし、像がこちらを向いているとすれば、左手を上げたように見えるはずです。
ここで、あなたが頭からかぶった黒い布を脱げば、鏡の像はあなたの顔がこちらを向いているのが見えますから、鏡像はこちらを向いていると判断します。つまり、私たちは鏡に映った私たちの姿に自分の前からの姿が見えるというだけ理由で、私たち自身が回れ右をして相対していると錯覚しているだけなのです。
つまり、鏡に映った像は、右は右、左は左、上は上、下は下とちゃんと反射している。つまり、あなたが右手を上げれば、鏡の像もちゃんと右手を上げている。つまり、鏡の像はこっちを向いているのはなく、向こうを向いていると考えれば、左右は逆転していません。
ただ、あなたの顔が映っているだけで、鏡に映った像があたかも、あなた自身が鏡の向こうの世界に行って、回れ右をしてこちらを向いていると錯覚してしまうのです。もっとわかりやすく言えば、鏡の像は向こうを向いていて、後頭部にあなたの顔を張り付けていると思えばいい。
これは「詭弁論理学」でも例として挙げられているのですが、黒く塗りつぶされたダンサーの像を鏡に映してみたらどうなるかという話があります。
ダンサーは黒く塗りつぶされているので、こっちを向いているのか向こうを向いているのかわかりません。もし、ダンサーがこちらを向いているのなら、左右が逆になるし、向こうを向いているのなら左右は逆にはなりません。
ただし、「詭弁論理学」では、そこから先の話が続かず、うやむやになってしまいました。
(ちなみに、黒く塗りつぶされたダンサーの図には「すべるジャネット・リン」と記載されていました。年配の方には懐かしい名前かもしれません。)
鏡文字はどうしてさかさま?
では、文字の場合はどうでしょう。文字を鏡に映すとまともに読めなくなってしまいますよね。つまり鏡文字です。ほらやっぱり、左右が逆になってしまうじゃないかと思われるかもしれません。
でもこれも目の錯覚なのです。例えば、アクリル板のような透明な板に文字を書いて鏡に映してみて下さい。確かに鏡に映った像は左右が反転してます。でも透明な板に書かれた文字も、こちら側からみれば反転していますよ。
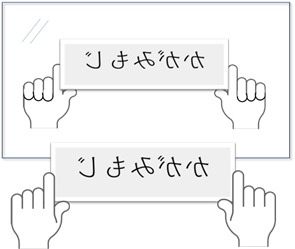
私たちは、普通、透明でない紙などに文字を書いて鏡に映します。実はこのとき、私たちは紙を裏返しにして鏡に映しているのです。この時点で、すでに文字は反転しています。だから鏡が反転させた文字を映しているわけではなく、わたしたちが文字を反転させて鏡に映しているということなのです。
この場合も、鏡は文字に対しても右は右、左は左、上は上、下は下と正確に反射させているのですが、私たち自身が文字を反転させて鏡に映しているわけです。つまり、この場合も鏡の文字は向こうを向いているということなのです。
ちょっと蛇足ですが、世の中には鏡文字を自在に書くことができる人がいるようです。有名なところでは、レオナルド・ダ・ビンチがそうですが、「不思議の国のアリス」を書いたルイス・キャロルもそうです。
「不思議の国のアリス」の続編が「鏡の国のアリス」でした。かれが鏡文字を書くことと何か関係があるのでしょう。ちなみに、かれは「詭弁論理学」の著者と同じく数学者でした。数学者は鏡が好きなのでしょうか。
2020年10月10日
【関連記事】
潮の満ち引き、月の引力に引かれる方が満潮になるという説明図は間違いです
すでに宇宙人が地球に来ている? 来ていないというこれだけの理由
アンコールワットはフランス人探検家が発見した? 西洋人が作り出したデマ


